Storing Santorini Positions
Last year I wrote about my newfound obssession with the board game Santorini, and surprise: I am still hooked! My lastest curiousity is how to efficiently represent board positions of unfinished games.
Santorini is played on a 5x5 board with 2 workers per player. Each turn a worker is moved and builds on an adjacent square up to a height of 4, the blue dome. The worker can hop up a single level or drop from any height. The goal is to move a worker onto a third-level building or block your opponent from being able to complete a move-and-build turn.
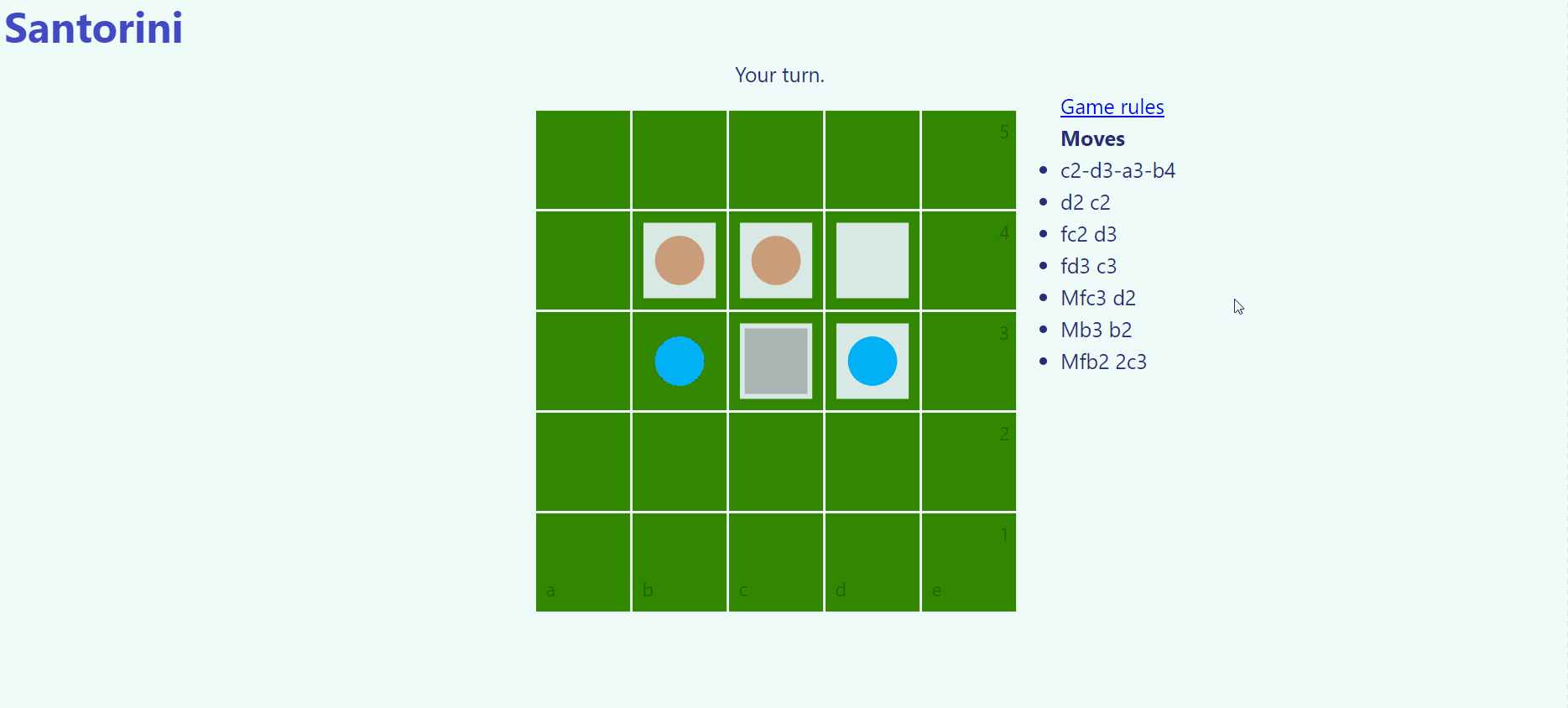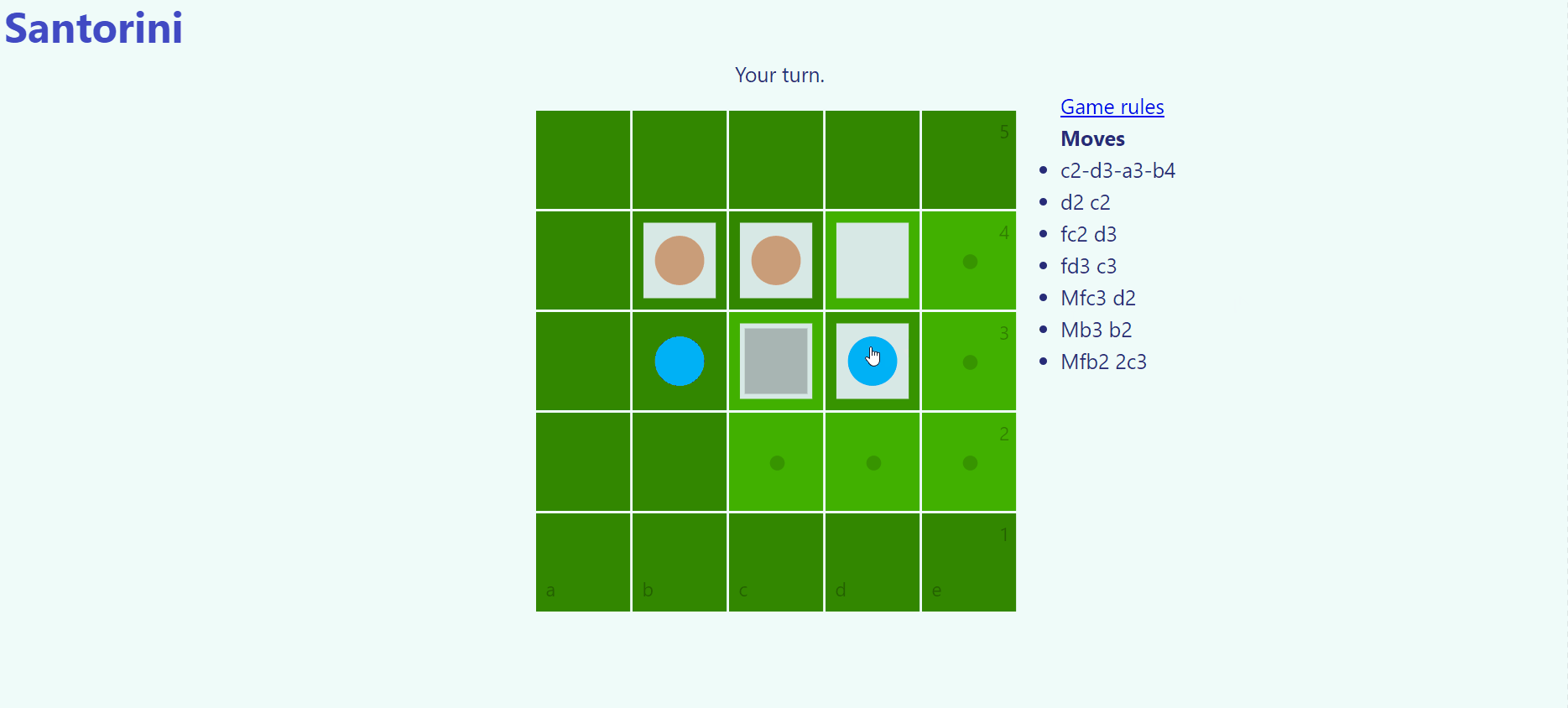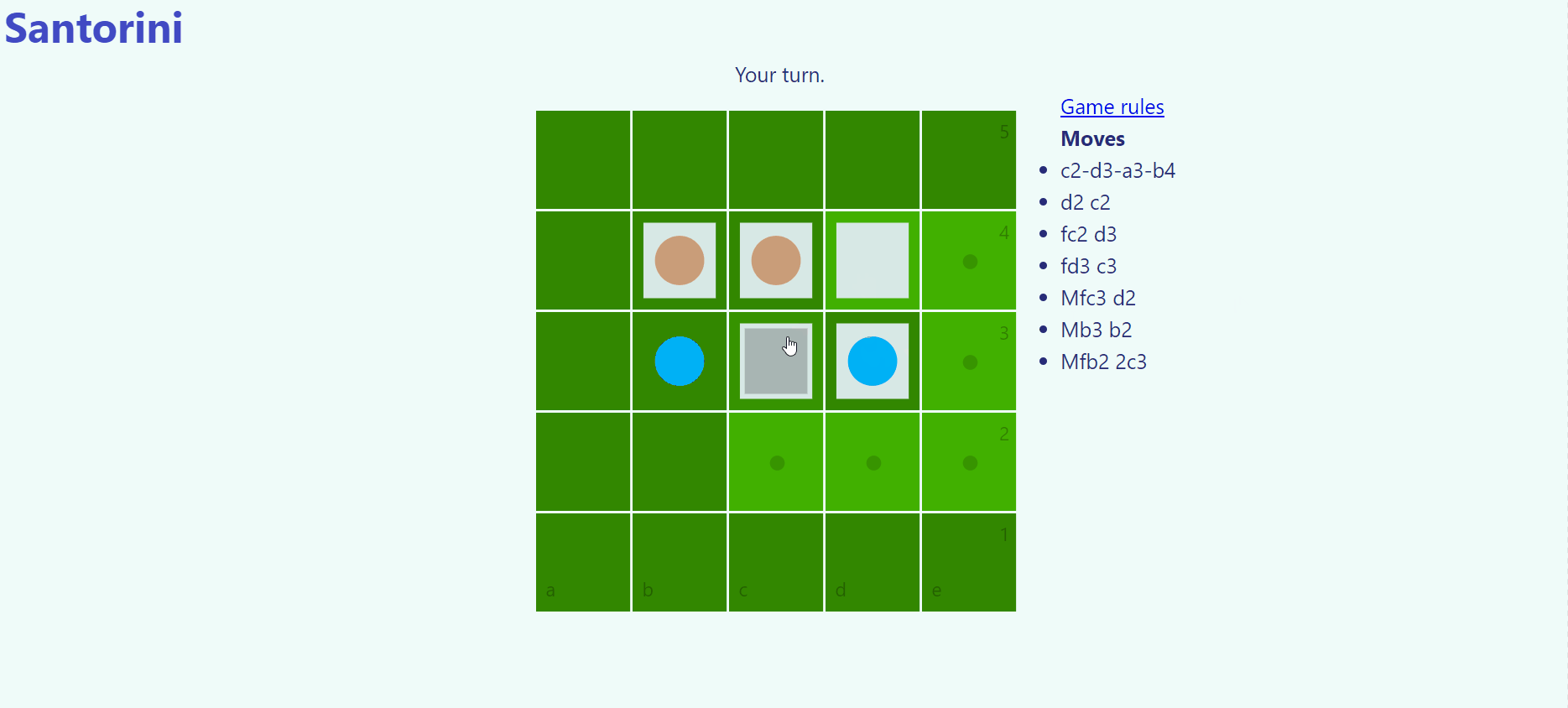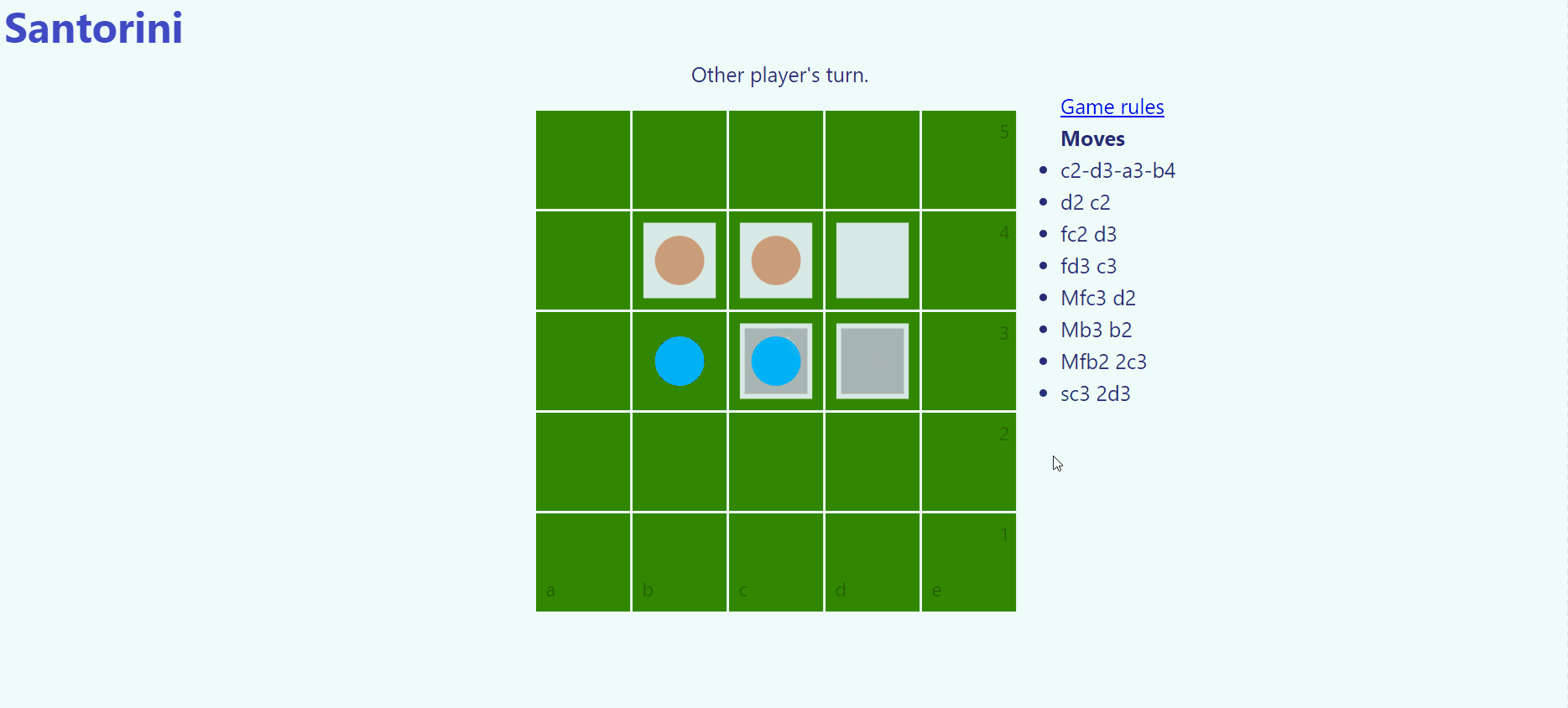
Example gameplay from the 2D Santorini clone I made.
First thoughts
A bit can represent whose turn it is. The value of 0 will be player one’s turn.
- 0: 1 bit for player turn
Next we must wrangle 25 board squares and 4 workers. We need 5 bits to count up to 25, meaning each worker needs 5 bits for its position. No worker can occupy the same square as another worker but this only gets us down to 21 possible squares for the last worker, saving us no bits.
- 00000: 5 bits for first worker’s square, 0 - 24
- 00000: 5 bits for second worker’s square, 0 - 23
- 00000: 5 bits for third worker’s square, 0 - 22
- 00000: 5 bits for fourth worker’s square, 0 - 21
20 bits for 4 worker positions. Next, the 25 squares, and I will only store squares with buildings. For convenience I will refer to the buildings of height one as Shops, two as Homes, three as Towers, and four as Domes. My first thought was to list the count of each building. Each type could max out though, and for an example of Shops that would mean all 25 squares. We need 5 bits to count up to 25.
- 00000 -> 5 bits for count of Shops, 0 - 24
- 00000 -> 5 bits for count of Homes, 0 - 24
- 00000 -> 5 bits for count of Towers, 0 - 21 (workers need to be on non-winning positions)
We’re at 15 bits for counting those buildings. We do not need to store Domes, and we’ll see why in a moment.
I thought next about having an uninterrupted list of building positions. For example, if the count was 2 Shops, 1 Home, and 1 Tower, we would parse the building coordinates in that order: 2 positions for Shops, 1 for a Home, and 1 for a Tower. The remaining positions can be assumed to be Domes.
- 00000 -> 5 bits per building position, 0 - 24
In a maximal unfinished case we now have a number for the bits to store the board:
- 1 + 20 + 15 + (25 * 5) = 161 bits
Tantalizingly close to an even 160 bits or 20 bytes. But can we go even lower?
Skipping used building squares
The first building needs to be placed somewhere between square 0 and square 24. If we index only the available squares from top left to bottom right, the next one is between 0 and 23. Then 0 and 22. With a mass of buildings, the number of bits required to represent their positions shrinks as we cut down the available squares.
For example, there was a building in the center on square 12. However, after it is stored, the next building would also be stored as square 12, because that’s the 12th available square at that time.
Instead of 25 * 5 or 125 bits to store all building positions, we can have:
- 0 through 9 positions: x * 5 = 0 to 45 bits
- 10 through 17 positions: 45 + x * 4 = 45 to 77 bits
- 18 through 21 positions: 77 + x * 3 = 77 to 89 bits
- 22 through 23 positions: 89 + x * 2 = 89 to 93 bits
- 24 through 25 positions: 93 + x * 1 = 93 to 95 bits
This cuts 30 bits off in the worst case for a new total of 131 bits made of:
- 1 bit for player turn
- 20 bits for worker positions
- 15 bits for building counts
- 95 bits for building positions
A full example
Let’s convert the following board state into the 131 bit format. Player one is blue.

Because it’s the first player’s turn, we will set the first bit to 0.
0
Next are the worker positions. Player one’s first worker is on square 6 and their second worker is on square 14. Player’s two are on 1 and 12, respectively. In binary:
- 6 = 00110
- 14 = 01110
- 1 = 00001
- 12 = 01100
Adding those we get:
0 00110 01110 00001 01100
The following 15 bits are for building counts. We have 1 Shop, 8 Homes, and 0 Towers.
- 1 = 00001
- 8 = 01000
- 0 = 00000
0 00110 01110 00001 01100 00001 01000 00000
Now for the last bits: all building positions. The first Shop is on available square 4 or 00100.
0 00110 01110 00001 01100 00001 01000 00000 00100
With that stored, the Homes are found on:
- Available square 1 = 00001
- Available square 4 = 00100
- Available square 5 = 00101
- Available square 7 = 00111
- Available square 7 = 00111
- Available square 7 = 00111
- Available square 7 = 00111
- Available square 9 = 01001
The final Dome is at the 10th position, allowing us to drop a bit to represent it among the 16 available squares left. We find it on available square 9 for our final 4 bits of 1001. Because we had the count of Shops, Homes, and Towers, we are able to assume any remaining positions are for domes.
0 00110 01110 00001 01100 00001 01000 00000 00100 00001 00100 00101 00111 00111 00111 00111 01001 1001
The example fits in a tidy 85 bits!
Practicality
I am going to use this to store and share Santorini puzzles for people to play out. Until that’s built out, feel free to play 2D Santorini or 3D Santorini locally or against friends via WebRTC.